Basic Math for Dice and Events¶
Basics of Dice and combinations¶
Rolling two six-sided dice provides a good introduction to the math behind die rolls. Below are all the possible ways to roll 2D6 grouped by the total roll:
2: 1-1
3: 1-2, 2-1
4: 1-3, 3-1, 2-2
5: 1-4, 4-1, 2-3, 3-2
6: 1-5, 5-1, 2-4, 4-2, 3-3
7: 1-6, 6-1, 2-5, 5-2, 3-4, 4-3
8: 2-6, 6-2, 3-5, 5-3, 4-4
9: 3-6, 6-3, 4-5, 5-4
10: 4-6, 6-4, 5-5
11: 5-6, 6-5,
12: 6-6
There is only one way to roll a “2”, but there are six ways to roll a “7”. There are a total of 36 different combinations on these two sets of dice. That means that your chance of rolling a 2 is 1/36 while your chance of rolling a 7 is 6/36.
You could test this with a quick piece of python code, like so:
from random import randint
def roll_six():
return randint(1, 6)
def ten_thousand_rolls_of_2d6():
answer = {roll: 0 for roll in range(2, 13)}
for _ in range(10000):
roll1 = roll_six()
roll2 = roll_six()
total= roll1 + roll2
answer[total] += 1
return answer
print(ten_thousand_rolls_of_2d6())
Running this scripts returned the following:
{2: 317,
3: 572,
4: 813,
5: 1135,
6: 1349,
7: 1635,
8: 1417,
9: 1123,
10: 805,
11: 548,
12: 286}
Of the 10,000 rolls, 12 was rolled 286 times, or 2.8% (pretty close to 1/36). 7 happened about 16% of the time (pretty close to 6/36).
Events Dictionary¶
While the above is great for visualization, it quickly becomes unmanageable. Imagine mapping out all the totals for 3D6 (there are 216 of them), or, even worse, having to keep track of 3 dice of 3 different sizes.
Instead, use dictionary of events having {roll: number_of_times_it_occurs}. On a six-sided die, each
roll has an equal chance of occurring, so it’s represented by the dictionary:
{1: 1, 2: 1, 3: 1, 4: 1, 5: 1, 6: 1}.
To combine this with another six-sided die,
you iterate through each die roll and create a new dictionary. When the second die rolls a “1”,
it bumps all the rolls up by one, making: {1+1: 1 ,2+1: 1, 3+1: 1, 4+1: 1, 5+1: 1, 6+1: 1}. When
the second die rolls a “2” it bumps all the die rolls up by two, making:
{1+2: 1 ,2+2: 1, 3+2: 1, 4+2: 1, 5+2: 1, 6+2: 1}. Keep doing this for each roll and add them up.
{2: 1, 3: 1, 4: 1, 5: 1, 6: 1, 7: 1}
{3: 1, 4: 1, 5: 1, 6: 1, 7: 1, 8: 1}
{4: 1, 5: 1, 6: 1, 7: 1, 8: 1, 9: 1}
{5: 1, 6: 1, 7: 1, 8: 1, 9: 1, 10: 1}
{6: 1, 7: 1, 8: 1, 9: 1, 10: 1, 11: 1}
+ {7: 1, 8: 1, 9: 1, 10: 1, 11: 1, 12: 1}
---------------------------------------------------------------------
{2: 1, 3: 2, 4: 3, 5: 4, 6: 5, 7: 6, 8: 5, 9: 4, 10: 3, 11: 2, 12: 1}
This dictionary of events is the spread of combinations for 2D6. It is the same as the other representation in the previous section. “2” has one combination, “3” has two combinations and “7” has six combinations.
Using this method, adding another six-sided die to 2D6 becomes much more manageable. Simply take the dictionary of 2D6 above, and for each roll of the next six-sided die, create a new dictionary of events.
When the third six-sided die rolls a “1”, you get:
{2+1: 1, 3+1: 2, 4+1: 3, 5+1: 4, 6+1: 5, 7+1: 6, 8+1: 5, 9+1: 4, 10+1: 3, 11+1: 2, 12+1: 1}
And when it rolls a “2”, you get:
{2+2: 1, 3+2: 2, 4+2: 3, 5+2: 4, 6+2: 5, 7+2: 6, 8+2: 5, 9+2: 4, 10+2: 3, 11+2: 2, 12+2: 1}
This makes:
{3: 1, 4: 2, 5: 3, 6: 4, 7: 5, 8: 6, 9: 5, 10: 4, 11: 3, 12: 2, 13: 1}
{4: 1, 5: 2, 6: 3, 7: 4, 8: 5, 9: 6, 10: 5, 11: 4, 12: 3, 13: 2, 14: 1}
{5: 1, 6: 2, 7: 3, 8: 4, 9: 5, 10: 6, 11: 5, 12: 4, 13: 3, 14: 2, 15: 1}
{6: 1, 7: 2, 8: 3, 9: 4, 10: 5, 11: 6, 12: 5, 13: 4, 14: 3, 15: 2, 16: 1}
{7: 1, 8: 2, 9: 3, 10: 4, 11: 5, 12: 6, 13: 5, 14: 4, 15: 3, 16: 2, 17: 1}
+ {8: 1, 9: 2, 10: 3, 11: 4, 12: 5, 13: 6, 14: 5, 15: 4, 16: 3, 17: 2, 18: 1}
-------------------------------------------------------------------------------------------------------------------
{3: 1, 4: 3, 5: 6, 6: 10, 7: 15, 8: 21, 9: 25, 10: 27, 11: 27, 12: 25, 13: 21, 14: 15, 15: 10, 16: 6, 17: 3, 18: 1}
Another example with 2D6:
Take 2d6 and add a different die to it. This time, it’s a weighted 2-sided die that rolls
“2” three times as often as “1”. This die is represented by the dictionary: {1: 1, 2: 3}.
Two 6-sided dice:
{2: 1, 3: 2, 4: 3, 5: 4, 6: 5, 7: 6, 8: 5, 9: 4, 10: 3, 11: 2, 12: 1}
A weighted 2-sided die:
{1: 1, 2: 3}
Applying a roll of “one” to two 6-sided dice:
A = {2+1: 1, 3+1: 2, 4+1: 3, 5+1: 4, 6+1: 5, 7+1: 6, 8+1: 5, 9+1: 4, 10+1: 3, 11+1: 2, 12+1: 1}
Applying a roll of “two” to two 6-sided dice:
B = {2+2: 1, 3+2: 2, 4+2: 3, 5+2: 4, 6+2: 5, 7+2: 6, 8+2: 5, 9+2: 4, 10+2: 3, 11+2: 2, 12+2: 1}
On this weighted die, “2” gets rolled 3 times as often as “1”. So you combine 1*A and 3*B:
{3: 1, 4: 2, 5: 3, 6: 4, 7: 5, 8: 6, 9: 5, 10: 4, 11: 3, 12: 2, 13: 1} # A
{4: 1, 5: 2, 6: 3, 7: 4, 8: 5, 9: 6, 10: 5, 11: 4, 12: 3, 13: 2, 14: 1} # B
{4: 1, 5: 2, 6: 3, 7: 4, 8: 5, 9: 6, 10: 5, 11: 4, 12: 3, 13: 2, 14: 1} # B
+ {4: 1, 5: 2, 6: 3, 7: 4, 8: 5, 9: 6, 10: 5, 11: 4, 12: 3, 13: 2, 14: 1} # B
-----------------------------------------------------------------------------------------
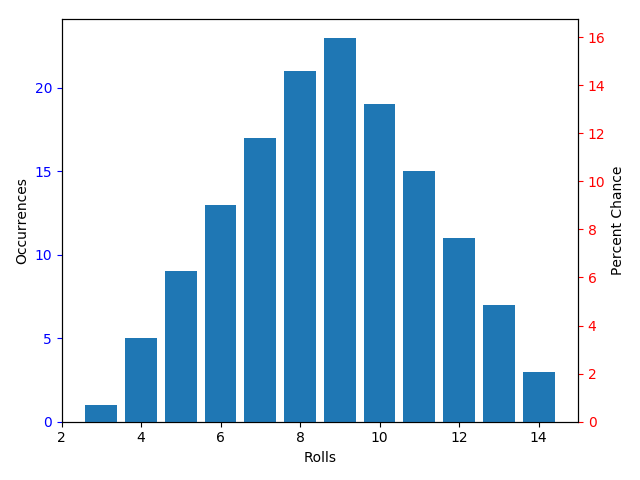
{3: 1, 4: 5, 5: 9, 6: 13, 7: 17, 8: 21, 9: 23, 10: 19, 11: 15, 12: 11, 13: 7, 14: 3}
So if you rolled 2D6 and 1WeightedDie({1: 1, 2: 3}). You’d get the following distribution. There are 144 total occurrences. 3 happens once, giving it a 0.69% chance, and 9 happens 23 times, giving you a 15.97% chance of rolling a 9.