The Dice

• Die Classes

• Dice Pools

• Some Example Dice

A die class is a dicetables.eventsbases.protodie.ProtoDie, which is a subclass of dicetables.eventsbases.integerevents.IntegerEvents. It is a representation of die.

All dice require implementations of the following methods:

• get_dict()The representation of the die rolls as {roll: frequency}.

  >>> import dicetables as dt
  >>> dt.Die(3).get_dict() == {1: 1, 2: 1, 3: 1}
  True
  >>> dt.ModDie(3, -2).get_dict() == {-1: 1, 0: 1, 1: 1}
  True
  

• get_size()The size of the die. This can occasionally be non-intuitive.

  >>> die = dt.WeightedDie({1: 1, 2: 1, 3: 0})
  >>> die.get_size()
  3
  >>> die.get_dict() == {1: 1, 2: 1}
  True
  

• get_weight(): The total weight of all the die rolls. Used mainly in the __lt__ method to differentiate between dice of equal size.

• weight_info(): A string detailing the rolls and their weights.

• multiply_str(number)The string representation for multiples of the die.

  >>> die = dt.ModDie(6, 1)
  >>> str(die)
  'D6+1'
  >>> die.multiply_str(5)
  '5D6+5'
  

• __str__()

• __repr__()

Dice are immutable , hashable and rich-comparable. Multiple names can safely point to the same instance of a Die, they can be used in sets and dictionary keys and they can be sorted with any other kind of die. Comparisons are done by (size, weight, get_dict, __repr__(as a last resort)). So:

>>> dice_list = [
... dt.ModDie(2, 0),
... dt.WeightedDie({1: 1, 2: 1}),
... dt.Die(2),
... dt.ModWeightedDie({1: 1, 2: 1}, 0),
... dt.StrongDie(dt.Die(2), 1),
... dt.StrongDie(dt.WeightedDie({1: 1, 2: 1}), 1)
... ]
>>> [die.get_dict() == {1: 1, 2: 1} for die in dice_list]
[True, True, True, True, True, True]
>>> sorted(dice_list)
[Die(2),
 ModDie(2, 0),
 StrongDie(Die(2), 1),
 ModWeightedDie({1: 1, 2: 1}, 0),
 StrongDie(WeightedDie({1: 1, 2: 1}), 1),
 WeightedDie({1: 1, 2: 1})]
>>> [die == dt.Die(2) for die in sorted(dice_list)]
[True, False, False, False, False, False]
>>> my_set = {dt.Die(6)}
>>> my_set.add(dt.Die(6))
>>> my_set == {dt.Die(6)}
True
>>> my_set.add(dt.ModDie(6, 0))
>>> my_set == {dt.Die(6), dt.ModDie(6, 0)}
True

Top

Die Classes

class dicetables.dieevents.Die(die_size: int)

stores and returns info for a basic Die. Die(4) rolls 1, 2, 3, 4 with equal weight

Base methods for all dice:

get_size()

get_weight()

get_dict() → Dict[int, int]

Returns

{event: occurrences}

weight_info()

return detailed info of how the die is weighted

multiply_str(number)

return a string that is the die string multiplied by a number. i.e., D6+1 times 3 is ‘3D6+3’

class dicetables.dieevents.ModDie(die_size: int, modifier: int)

stores and returns info for a Die with a modifier that changes the values of the rolls. ModDie(4, -1) rolls 0, 1, 2, 3 with equal weight

It is 4-sided die with -1 added to each roll (D4-1)

added methods:

get_modifier() → int

class dicetables.dieevents.WeightedDie(dictionary_input: Dict[int, int])

stores and returns info for die with different chances for different rolls. WeightedDie({1:1, 2:5}) rolls 1 once for every five times that 2 is rolled.

dt.WeightedDie({1:1, 3:3, 4:6}) is a 4-sided die. It rolls 4 six times as often as 1, rolls 3 three times as often as 1 and never rolls 2

added methods:

get_raw_dict() → Dict[int, int]

get_raw_dict() returns something similar to the input dict with keys from 1 to die.get_size() even if they are zero. dt.WeightedDie({1: 1, 3: 3, 4: 6}).get_raw_dict() returns {1: 1, 2: 0, 3: 3, 4: 4}

class dicetables.dieevents.ModWeightedDie(dictionary_input: Dict[int, int], modifier: int)

stores and returns info for die with different chances for different rolls. The modifier changes all die rolls. ModWeightedDie({1:1, 3:5}, -1) is a 3-sided die - 1. It rolls 0 once for every five times that 2 is rolled.

added methods:

get_modifier() → int

get_raw_dict() → Dict[int, int]

>>> dt.WeightedDie({1: 1, 3: 3, 4: 6}).get_raw_dict() == {1: 1, 2: 0, 3: 3, 4: 6}
True
>>> dt.ModWeightedDie({1: 1, 3: 3, 4: 6}, -100).get_raw_dict() == {1: 1, 2: 0, 3: 3, 4: 6}
True

class dicetables.dieevents.StrongDie(input_die: dicetables.eventsbases.protodie.ProtoDie, multiplier: int)

stores and returns info for a stronger version of another die (including StrongDie if you’re feeling especially silly). The multiplier multiplies all die rolls of original Die. StrongDie(ModDie(3, -1), 2) rolls (1-1)*2, (2-1)*2, (3-1)*2 with equal weight.

>>> die = dt.Die(4)
>>> die.get_dict() == {1: 1, 2: 1, 3: 1, 4: 1}
True
>>> dt.StrongDie(die, 5).get_dict() == {5: 1, 10: 1, 15: 1, 20: 1}
True
>>> example = dt.StrongDie(die, -2)
>>> example.get_dict() == {-2: 1, -4: 1, -6: 1, -8: 1}
True
>>> example.get_input_die() == die
True
>>> example.get_multiplier()
-2

added methods:

get_multiplier()

get_input_die() → dicetables.eventsbases.protodie.ProtoDie

returns an instance of the original die

class dicetables.dieevents.Modifier(modifier: int)

stores and returns info for a modifier to add to the final die roll. Modifier(-3) rolls -3 and only -3. A Modifier’s size and weight are always 0.

>>> table = dt.DiceTable.new().add_die(dt.Die(4))
>>> table.get_dict() == {1: 1, 2: 1, 3: 1, 4: 1}
True
>>> table = table.add_die(dt.Modifier(3))
>>> print(table)
+3
1D4
>>> table.get_dict() == {4: 1, 5: 1, 6: 1, 7: 1}
True

added methods:

get_modifier() → int

class dicetables.dieevents.Exploding(input_die: dicetables.eventsbases.protodie.ProtoDie, explosions: int = 2)

Stores and returns info for an exploding version of another die. Each time the highest number is rolled, you add that to the total and keep rolling. An exploding D6 rolls 1-5 as usual. When it rolls a 6, it re-rolls and adds that 6. If it rolls a 6 again, this continues, adding 12 to the result. Since this is an infinite but increasingly unlikely process, the “explosions” parameter sets the number of re-rolls allowed.

Explosions are applied after modifiers and multipliers. Exploding(ModDie(4, -2)) explodes on a 2 so it rolls: [-1, 0, 1, (2 -1), (2 + 0), (2 + 1), (2+2 - 1) ..]

WARNING: setting the number of explosions too high can make instantiation VERY slow. The time is proportional to explosions and die_size.

Here are the rolls for an exploding D4 that can explode up to 3 times. It rolls 1-3 sixty-four times more often than 13-16.

>>> roll_values = dt.Exploding(dt.Die(4), explosions=3).get_dict()
>>> sorted(roll_values.items())
 [(1, 64), (2, 64), (3, 64),
  (5, 16), (6, 16), (7, 16),
  (9, 4), (10, 4), (11, 4),
  (13, 1), (14, 1), (15, 1), (16, 1)]

Any modifiers and multipliers are applied to each re-roll. Exploding D6+1 explodes on a 7. On a “7” it rolls 7 + (D6 + 1). On a “14”, it rolls 14 + (D6 + 1).

Here are the rolls for an exploding D6+1 that can explode the default times.

>>> roll_values = dt.Exploding(dt.ModDie(6, 1)).get_dict()
>>> sorted(roll_values.items())
[(2, 36), (3, 36), (4, 36), (5, 36), (6, 36),
 (9, 6), (10, 6), (11, 6), (12, 6), (13, 6),
 (16, 1), (17, 1), (18, 1), (19, 1), (20, 1), (21, 1)]

added methods:

get_explosions() → int

get_input_die() → dicetables.eventsbases.protodie.ProtoDie

returns an instance of the original die

class dicetables.dieevents.ExplodingOn(input_die: dicetables.eventsbases.protodie.ProtoDie, explodes_on: Iterable[int], explosions: int = 2)

Stores and returns info for an exploding version of another die. Each time the values in (explodes_on) are rolled, the die continues to roll, adding that value to the result. The die only continues rolling an (explosions) number of times.

ExplodingOn(Die(6), (1, 6), explosions=2) rolls: [2 to 5], 1+[2 to 5], 6+[2 to 5], 1+1+[1 to 6], 1+6+[1 to 6], 6+1+[1 to 6] and 6+6+[1 to 6].

Explosions are applied after modifiers and multipliers. ExplodingOn(ModDie(4, -2), (2,)) explodes on a 2 so it rolls: [-1, 0, 1, (2 -1), (2 + 0), (2 + 1), (2+2 - 1) ..]

WARNING: setting the number of explosions too high can make instantiation VERY slow. Time is proportional to explosion**(len(explodes_on)). It’s also linear with size which gets overshadowed by the first factor.

Here are the rolls for an exploding D6 that can explode the default times and explodes on 5 and 6.

>>> roll_values = dt.ExplodingOn(dt.Die(6), (5, 6)).get_dict()
>>> sorted(roll_values.items())
[(1, 36), (2, 36), (3, 36), (4, 36),
 (6, 6), (7, 12), (8, 12), (9, 12), (10, 6),
 (11, 1), (12, 3), (13, 4), (14, 4), (15, 4), (16, 4), (17, 3), (18, 1)]

added methods:

get_explosions()

get_explodes_on() → Tuple[int, …]

get_input_die() → dicetables.eventsbases.protodie.ProtoDie

returns an instance of the original die

Top

Dice Pools

DicePool s are a pool of a single die. DicePoolCollection s are lightweight wrappers around a DicePool. They are a way to extract rolls from a Dice Pool and cast it as a ProtoDie. DicePool can be expensive to instantiate, which is explained below. They are immutable and a single instance can be passed to many collections.

class dicetables.dicepool.DicePool(input_die: dicetables.eventsbases.protodie.ProtoDie, pool_size: int)

property die

property size

property rolls

The collections are treated as one giant Die with very funky rolling behavior. They all follow the basic form: <WhatToSelect>OfDicePool(pool=DicePool(input_die, pool_size), select=<int>). BestOfDicePool(DicePool(Die(6), 4), 3) means: Make a dice pool of 4D6. Roll this and take the best three results from every roll. This object is also an 18-sided “Die” that rolls from 3 to 18.

class dicetables.dicepool_collection.DicePoolCollection(pool: dicetables.dicepool.DicePool, select: int)

The abstract class for all DicePoolCollection objects. A DicePoolCollection creates a new die by selecting from a DicePool. Select determines how many rolls are selected from the pool of total rolls. Different implementations determine which particular rolls to select.

get_pool() → dicetables.dicepool.DicePool

get_select() → int

class dicetables.dicepool_collection.BestOfDicePool(pool: dicetables.dicepool.DicePool, select: int)

Take the best [select] rolls from a DicePool of [pool_size] * [input_die]. BestOfDicePool(DicePool(Die(6), 4), 3) is the best 3 rolls from four six-sided dice.

class dicetables.dicepool_collection.WorstOfDicePool(pool: dicetables.dicepool.DicePool, select: int)

Take the worst [select] rolls from a DicePool of [pool_size] * [input_die]. WorstOfDicePool(DicePool(Die(6), 4), 3) is the worst 3 rolls from four six-sided dice.

class dicetables.dicepool_collection.UpperMidOfDicePool(pool: dicetables.dicepool.DicePool, select: int)

Take the middle [select] rolls from a DicePool of [pool_size] * [input_die]. UpperMidOfDicePool(DicePool(Die(6), 5), 3) is the middle 3 rolls from five six-sided dice.

If there is no perfect middle, take the higher of two choices. For five dice that roll (1, 1, 2, 3, 4), select=3 takes (1, 2, 3) and select=2 takes (2, 3).

class dicetables.dicepool_collection.LowerMidOfDicePool(pool: dicetables.dicepool.DicePool, select: int)

Take the middle [select] rolls from a DicePool of [pool_size] * [input_die]. LowerMidOfDicePool(DicePool(Die(6), 5), 3) is the middle 3 rolls from five six-sided dice.

If there is no perfect middle, take the lower of two choices. For five dice that roll (1, 1, 2, 3, 4), select=3 takes (1, 2, 3) and select=2 takes (1, 2).

All DicePool objects calculate all the possible combinations of rolls and the frequency of each combination. So, DicePool(Die(3), 3, 2) creates the following dictionary

>>> pool = dt.DicePool(dt.Die(3), 3)
>>> pool.rolls == {
... (1, 1, 1): 1,
... (1, 1, 2): 3,
... (1, 1, 3): 3,
... (1, 2, 2): 3,
... (1, 2, 3): 6,
... (1, 3, 3): 3,
... (2, 2, 2): 1,
... (2, 2, 3): 3,
... (2, 3, 3): 3,
... (3, 3, 3): 1
... }
True

This says that, with 3*Die(3), the roll: (1, 1, 1) happens once. The roll: (1, 2, 3) happens 6 times. BestOfDicePool(DicePool(Die(3), 3), 2) looks at the above dictionary and selects the two best rolls in each tuple. so:

>>> best_two = dt.BestOfDicePool(pool, 2)
>>> best_two.get_dict() == {2: 1, 3: 3, 4: 7, 5: 9, 6: 7}
True

The number of keys in any one of these dictionaries relies on pool_size and dict_size = len(input_die.get_dict()). The formula is (dict_size-1 + pool_size)!/(dict_size-1)! * 1/(pool_size)! and you can calculate it using count_unique_combination_keys. If you have a key_count, you can find the pool_size with largest_permitted_pool_size.

>>> from dicetables.tools.orderedcombinations import count_unique_combination_keys, largest_permitted_pool_size
>>> count_unique_combination_keys(dt.Die(3), 3) == 10  # The dictionary demonstrated above
True
>>> count_unique_combination_keys(dt.Die(6), 10) == 3003
True
>>> count_unique_combination_keys(dt.Die(6), 20) == 53130
True
>>> count_unique_combination_keys(dt.Die(6), 30) == 324632
True
>>> largest_permitted_pool_size(dt.Die(6), 330000)
30

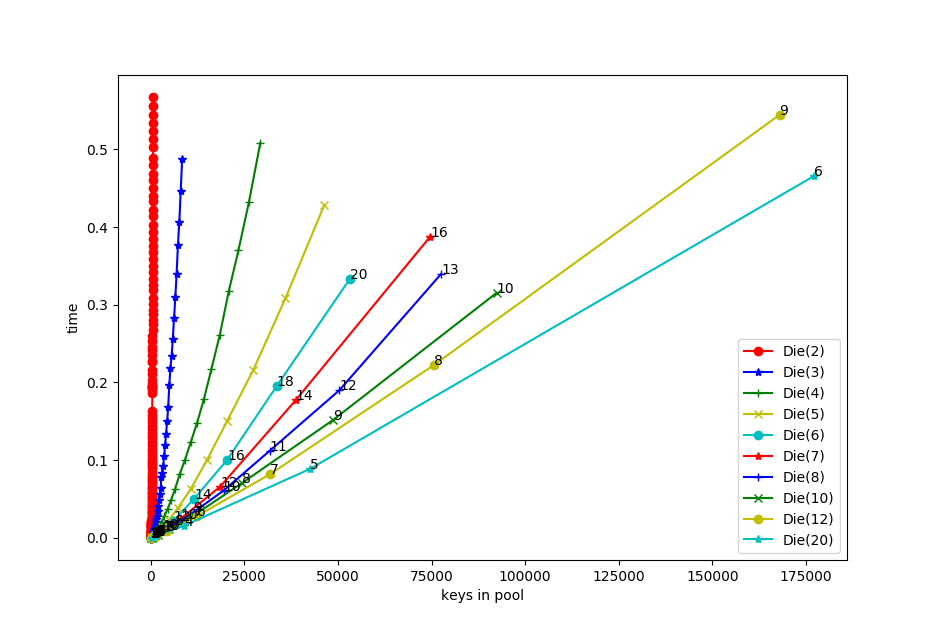
This graph gives an idea of the times to instantiate different DicePools. It is time vs number-of-keys-needed-to-generate-the-pool. The black annotations are the pool sizes. Notice that each of these increases linearly with the underlying dictionary, but closer to exponentially with pool_size. Especially with larger dice, an increase of one in the pool size can have a surprisingly large effect.

Some Example Dice

• WeightedDie({1: 3, 2: 4, 3: 4, 4: 4, 5: 4, 6: 5}) a mildly weighted die that has a 21% chance to roll a “6” (5/24), a 12.5% chance to roll a “1” and the rest are 1 in 6 (4/24).

• ModWeightedDie({1: 3, 2: 1, 3: 1, 4: 1}, -1) a six-sided die with faces [0, 0, 0, 1, 2, 3].

• ModDie(2, -1) a coin where “1” is heads, and “0” is tails. The die roll will tell you the number of heads rolled.

• ModWeightedDie({1: 40, 2: 60}, -1) a cheater’s coin that rolls heads 60% of the time.

• ModWeightedDie({1: 45, 2: 55}. -1) a person who’s likely to pick “1” 55% of the time.

• StrongDie(ModWeightedDie({1: 10, 2: 90}, -1), 1000) a thousand people who will almost certainly choose “1” and will all vote as a block. whatever they choose, they’re doing it as a team.

• BestOfDicePool(DicePool(Die(6), 4), 3) best 3 out of 4D6.

• 2 Die(6) and Modifier(3) 2D6+3

  >>> import dicetables as dt
  >>> dt.DiceTable.new().add_die(dt.Die(6), 2).add_die(dt.Modifier(3))
  <DiceTable containing [+3, 2D6]>
  

Top